LQR Controller Design¶
The controller to be implemented is a full-state feedback controller. The LQR controller was selected. Fig. 4 shows the block diagram of the entire system to be implemented.
![digraph {
graph [rankdir=LR, splines=ortho, concentrate=true];
node [shape=polygon];
node[group=main];
System [ label="Segway \n ẋ = Ax(t) + Bu(t)", rank=1];
i [shape=point];
x [shape=plaintext, label=""];
C [ label="C" ];
y [shape=plaintext, label=""];
System -> i [ dir="none", label="x(t)" ];
i -> C;
C -> y [ label="y(t)"];
node[group="feedback"];
Feedback [ label="-K", rank=1 ];
Feedback -> System [ label="u(t)"];
Feedback -> i [ dir=back ];
}](../_images/graphviz-b85ebafd22aff9b1cfca84018b77de7945e226dc.png)
Fig. 4 Full-state feedback block diagram¶
Physical parameters¶
All the parameters needed for the model can be seen in Listing 6
% Sampling constants
T_s = 20e-3;
f_s = 1/T_s;
% Constants (context)
m = 0.24200; % Mass of the zumo
m_1 = 0;
m_2 = m;
L_1 = 0;
L_2 = 0.062;
L = L_2/2 + (L_1 + L_2) * m_1/(2*m); % Height of the zumo
beta_m = 0.01;
beta_gamma = 0.01;
g = 9.8100; % Gravitational constant
R = 0.019; % Wheel radius
I = m_1*(L_1/2 + L_2)^2 + (m_2*L_2^2)/12; % Inertial momentum
m_w = 0.004; % Mass of the wheel
m_c = 0.009; % Mass of the caterpillar band
I_w_i = m_w*R^2; % Inertia momentum of wheels
I_c = m_c*R^2; % Inertia momentum of Caterpillar band
I_w = 2*I_w_i + I_c; % Inertia momentum of Caterpillar system
% Motor's constants
motor_stall_torque = 0.211846554999999; % According to specs 30 oz-in
pulse2torque = motor_stall_torque/400;
Note
For \(\beta_m\) and \(\beta_\gamma\) are set to a dummy value as in [15].
Model¶
To setup the model the script in Listing 7 was used.
function model = get_ssmodel()
% Consants (context)
load_physical_constants
E = [(I_w + (m_w + m)*R^2) m*R*L;
m*R*L (I + m*L^2)];
F = [(beta_gamma + beta_m) -beta_m;
-beta_m beta_m];
G = [0; -m*g*L];
H_1 = [1; -1] * pulse2torque;
states = size(E, 1);
A = [zeros(states) eye(states);
zeros(states, 1) -inv(E)*G -inv(E)*F];
B = [zeros(states, 1);
-inv(E)*H_1];
C = [1 0 0 0;
0 1 0 0;
0 0 1 0;
0 0 0 1];
D = [0; 0; 0; 0];
model = ss(A, B, C, D);
end
A second script, shown in Listing 8 was also added to get the model that also obtains the transfer function \(H(s) = \frac{\Theta(s)}{S(s)}\). Where, \(S(s)\) is the Laplace transform of the \(speed_{PWM}\) function. This transfer function was used to further analysis not presented in this documentation.
Controllability¶
Before the actually designing the controller we need to check it’s controllability. The controllability check done can be seen in Listing 9.
Observability¶
Similarly, the system’s observability has to be also verified. This verification is shown in Listing 10.
Control Law¶
To obtain the control law \(K\) the script in Listing 11.
Q = eye(size(model.a,1));
R = 1
[K, X, P] = lqr(model, Q, R);
K_s = K*pi/180;
Note
- As in [15] equally weighted states and outputs were used. Therefore, \(Q = I\) and \(R = 1\). Where, \(I\) is an identity matrix with the size of \(A\).
- A scaled control law \(K_s\) is also calculated. The scale factor is needed because the angles measured by accelerometer/gyro and encoders was done in degrees.
The obtained control law is shown in (11). And the scaled version in (12)
Controller Simulation¶
After designing the control law the controller is simulated as shown in Listing 12.
Ac = model.a - model.b*K;
sys_cl = ss(Ac, model.b, model.c, model.d);
figure(1);
clf(1)
impulse(sys_cl);
The simulation results can be seen in Fig. 5. Since the \(\frac{d\varphi}{dt}\) and \(\frac{d\theta}{dt}\) are faster variables a zoomed result simulation result can also be seen in Fig. 6.
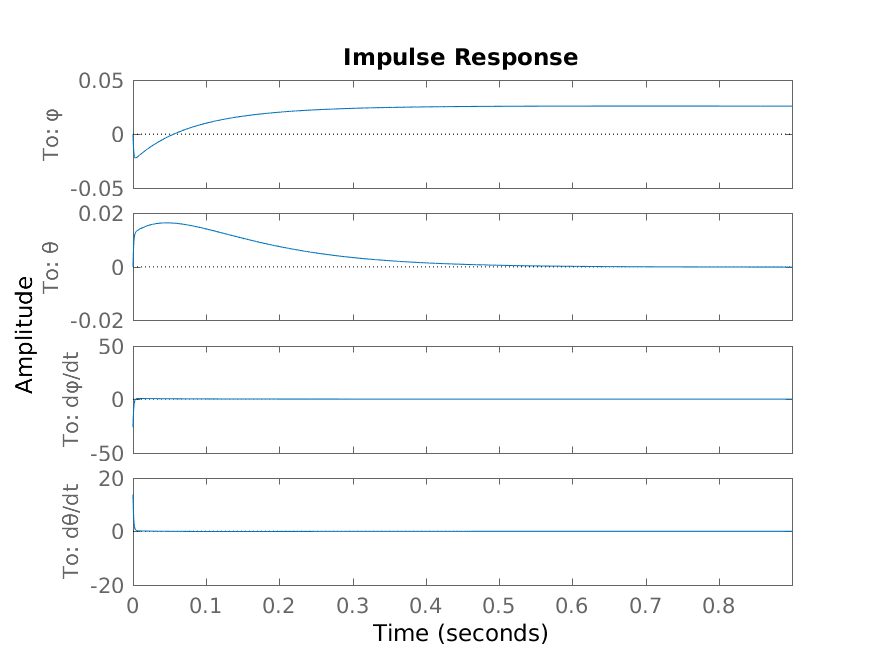
Fig. 5 LQR Design Simulation Results
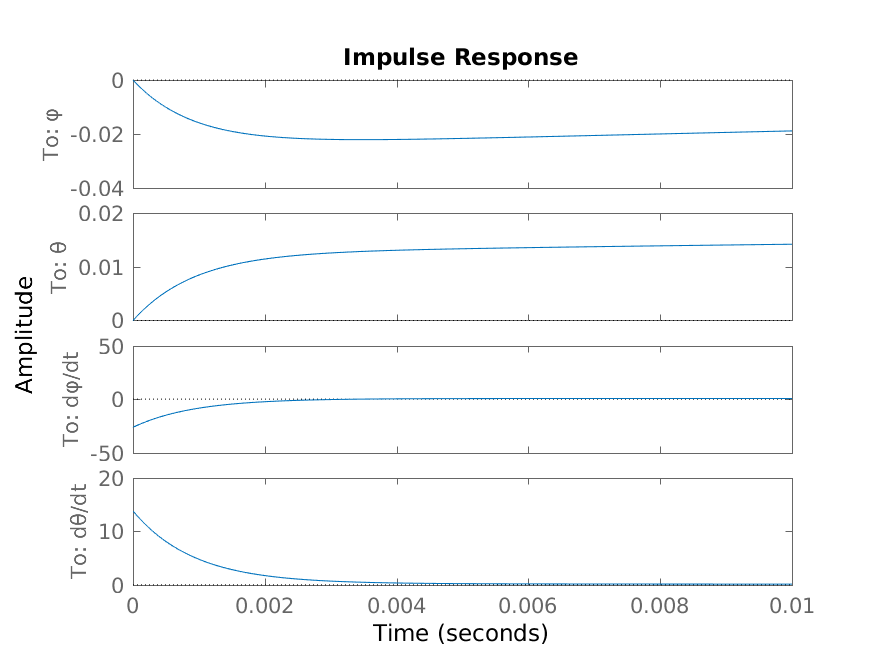
Fig. 6 LQR Design Zoomed Simulation Results
Further Features¶
Arduino Pretty Printing¶
For rapid deployment and testing the scripts/lqr_design.m also prints the scaled control law in the Arduino language. An example output can be seen in Listing 14 and the script excerpt that implement this functionality in Listing 13.
disp("Control Law")
K_string = strcat("const float K[", num2str(size(model.a,1)), "] = {");
for k = 1:size(K, 2)
if ~(k == 1)
K_string = strcat(K_string, ", ");
end
K_string = strcat(K_string, num2str(K_s(k)));
end
K_string = strcat(K_string, "};");
disp("K")
disp(K_string)
Control Law
K
const float K[4] = {0.017453, 8.4406, 0.1746, 0.35439}
Closed-Loop Poles¶
scripts/lqr_design.m also print out the closed-loop poles. An example output can be seen in Listing 15.
P =
1.0e+03 *
-1.0872
-0.0000
-0.0083
-0.0178
Full-compensator design¶
In scripts/lqr_design.m the full compensator design flow is implemented but since it’s not being implements it’s was left out of this documentation.
| [1] | (1, 2, 3, 4, 5, 6, 7, 8) Pedro Cuadra Meghadoot Gardi. Pjcuadra/zumogetway. August 2017. URL: https://github.com/pjcuadra/zumosegway. |
| [15] | (1, 2) Mie Kunio Ye Ding, Joshua Gafford. Modeling, simulation and fabrication of a balancing robot. Technical Report, Harvard University, Massachusettes Institute of Technology, 2012. |